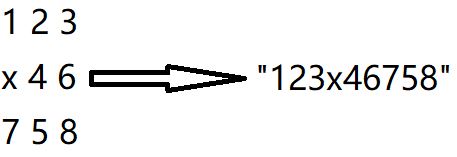博学之，审问之，慎思之，明辨之，笃行之。

第三章 搜索与图论

一、DFS

全排列问题(按字典序)：

详情：https://www.acwing.com/problem/content/844/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<iostream>
#include<vector>
using namespace std;
int a[10],n;
vector<int> path;
bool st[10];

void dfs(int u){
    if(u==n) {
        for(auto x : path) cout<<x<<' ';
        cout<<endl;
        return ;
    }
    
    for(int i=1;i<=n;i++){
        if(!st[i]) {
            st[i]=true;
            path.push_back(i);
            dfs(u+1);
            path.pop_back();
            st[i]=false;
        }
    }
}

int main(){
    cin>>n;
    dfs(0);
    return 0;
}

n皇后问题

详情：https://www.acwing.com/problem/content/845/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>
#include<cstring>
using namespace std;
const int N=20;
bool col[N],dg[N],udg[N];
int n;
char path[N][N];

void dfs(int u){
    if(u==n) {
        for(int i=0;i<n;i++) puts(path[i]);
        cout<<endl;
        return ;
    }
    
    for(int i=0;i<n;i++){
        if(!col[i] && !dg[u-i+n] && !udg[u+i]){
            path[u][i]='Q';
            col[i]=dg[u-i+n]=udg[u+i]=true;
            dfs(u+1);
            path[u][i]='.';
            col[i]=dg[u-i+n]=udg[u+i]=false;
        }
    }
}

int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++)
            path[i][j]='.';
    }
    dfs(0);
    return 0;
}

二、BFS

走迷宫问题

详情：https://www.acwing.com/problem/content/846/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
// BFS解法
#include<iostream>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
typedef pair<int,int> PII;
const int N=110;
int d[N][N],map[N][N];
int n,m;
queue<PII> q;
//PII pre[N][N];
int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};

int bfs(int x,int y){
    memset(d,-1,sizeof d);
    d[0][0]=0;
    q.push({0,0});
    while(q.size()){
        auto t=q.front();
        q.pop();
        for(int i=0;i<4;i++){
            int a=t.first+dx[i],b=t.second+dy[i];
            if(a<0 || a>=n || b<0 || b>=m || map[a][b]==1 || d[a][b]!=-1) continue;
            q.push({a,b});
            //pre[a][b]=t;
            d[a][b]=d[t.first][t.second]+1;
        }
    }
    
    // 输出路径
    // int a=n-1,b=m-1;
    // while(a || b){
    //     cout<<a<<' '<<b<<' '<<endl;
    //     auto t=pre[a][b];
    //     a=t.first,b=t.second;
    // }
    
    return d[n-1][m-1];
}

int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            cin>>map[i][j];
        }
    }
    cout<<bfs(0,0);
    
    return 0;
}

最少操作问题之“八数码”----数字华容道

此类问题难点在于抽象成bfs问题

详情：https://www.acwing.com/problem/content/847/

Q1：如何抽象出“节点”，用什么数据结构存储？

Q2：如何记录每个状态的“距离”（即需要移动的次数）？

Q3：队列如何定义？

A1：由初始状态进行多次变换得到的状态可以抽象成一个节点，将其用string存储，映射如下：

表示方法.JPG

同时给出矩阵与字符串的转换方式：

矩阵转换.JPG

A2：开一个哈希表，unordered_map<string,int> 后者int代表每个状态到初始状态的距离

A3：queue<string>

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<iostream>
#include<algorithm>
#include<queue>
#include<unordered_map>
using namespace std;
string start; // 定义初始状态
string End="12345678x";  // 定义目标状态
unordered_map<string,int> d;  // 定义dist哈希表，存储每个状态和距离
int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0}; // 偏移量，即转移方式

int bfs(string start){
    queue<string> q;
    q.push(start);
    d[start]=0;
    while(q.size()){
        auto t=q.front();
        q.pop();
        
        int distance=d[t];
        if(t==End) return distance;
        // 状态转移
        int k=t.find('x'); 
        int x=k/3,y=k%3;
        for(int i=0;i<4;i++){
            int a=x+dx[i],b=y+dy[i];
            if(a<0 || a>=3 || b<0 || b>=3) continue;
            swap(t[k],t[3*a+b]);
            if(!d.count(t)){ // 判重
                d[t]=distance+1;
                q.push(t);
            }
            swap(t[k],t[3*a+b]); // 需要恢复到变换之前的状态
        }
    }
    return -1;
}

int main(){
    for(int i=0;i<9;i++) {
        char ch;
        cin>>ch;
        start+=ch;
    }
    cout<<bfs(start)<<endl;
    return 0;
}

三、树和图

树和图的存储

树是一种特殊的无环联通图，故都可以用图的存储来表示

有向图：a------>b

无向图：a--------b

无向图是特殊的有向图

有向图的存储方式：

  • 邻接矩阵：g[a][b] 代表从a 到b 存在一条有向边

  • 邻接表：

    • 数组模拟存储：h[N], e[N], ne[N], idx

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      const int N=100010, M=2*N;

      int h[N], e[M], ne[M], idx;

      void add(int a,int b){
          e[idx]=b,ne[idx]=h[a],h[a]=idx++;
      }

      int main(){
          memset(h,-1,sizeof h);
      }

    • vector存储

      1
      2
      3
      const int N=100010;
      vector<int,vector<int>> h[N][N];
      h[a][b]=x;

树和图的遍历

深度优先遍历

1
2
3
4
5
6
7
void dfs(int u){
    st[u]=true; // 标记一下已经被搜过了
    for(int i=h[u];i!=-1;i=ne[i]){
        int j=e[i];
        if(!st[j]) dfs(j);
    }
}
树的重心：

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

详情：https://www.acwing.com/problem/content/848/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10; //数据范围是10的5次方
const int M = 2 * N; //以有向图的格式存储无向图，所以每个节点至多对应2n-2条边

int h[N]; //邻接表存储树，有n个节点，所以需要n个队列头节点
int e[M]; //存储元素,下标为i的点的编号
int ne[M]; //存储列表的next值
int idx; //单链表指针
int n; //题目所给的输入，n个节点
int ans = N; //表示重心的所有的子树中，最大的子树的结点数目
bool st[N]; //记录节点是否被访问过，访问过则标记为true

//a所对应的单链表中插入b  a作为根 
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

//返回以u为根的子树中节点的个数，包括u节点
int dfs(int u) {
    int res = 0; //存储 删掉某个节点之后，最大的连通子图节点数
    st[u] = true; //标记访问过u节点
    int sum = 1; //存储 以u为根的树 的节点数, 包括u，如图中的4号节点

    //访问u的每个子节点
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        //因为每个节点的编号都是不一样的，所以 用编号为下标 来标记是否被访问过
        if (!st[j]) {
            int s = dfs(j);  // u节点的单棵子树节点数 如图中的size值
            res = max(res, s); // 记录最大联通子图的节点数
            sum += s; //以j为根的树 的节点数
        }
    }

    //n-sum 如图中的n-size值，不包括根节点4；
    res = max(res, n - sum); // 选择u节点为重心，最大的 连通子图节点数
    ans = min(res, ans); //遍历过的假设重心中，最小的最大联通子图的 节点数
    return sum;
}

int main() {
    memset(h, -1, sizeof h); //初始化h数组 -1表示尾节点
    cin >> n; //表示树的结点数

    // 题目接下来会输入，n-1行数据，
    // 树中是不存在环的，对于有n个节点的树，必定是n-1条边
    for (int i = 0; i < n - 1; i++) {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a); //无向图
    }

    dfs(1); //可以任意选定一个节点开始 u<=n，为何不能选0开始，因为u是编号，在add函数中h[0]是没有意义的

    cout << ans << endl;

    return 0;
}

宽度优先遍历

记住：树和图的宽度优先遍历基本都用邻接表，不要和走迷宫的题混淆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <cstring>
#include <iostream>
using namespace std;
const int N=1e5+10;

int h[N], e[N], idx, ne[N];
int d[N]; //存储每个节点离起点的距离，也作为判重数组
int n, m; //n个节点m条边
int q[N]; //存储层次遍历序列 0号节点是编号为1的节点

void add(int a, int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

int bfs()
{
    int hh=0,tt=0;

    q[0]=1; //0号节点是编号为1的节点

    memset(d,-1,sizeof d);

    d[1]=0; //存储每个节点离起点的距离

    //当我们的队列不为空时
    while(hh<=tt)
    {
        //取出队列头部节点
        int t=q[hh++];

        //遍历t节点的每一个邻边
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            //如果j没有被扩展过
            if(d[j]==-1)
            {
                d[j]=d[t]+1; //d[j]存储j节点离起点的距离，并标记为访问过
                q[++tt] = j; //把j结点 压入队列
            }
        }
    }
    return d[n];
}

int main()
{
    cin>>n>>m;
    memset(h,-1,sizeof h);
    for(int i=0;i<m;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
    }
    cout<<bfs()<<endl;
}
拓扑排序

有向无环图（拓扑图）才有拓扑序

详情：https://www.acwing.com/problem/content/850/

核心思路：

  • 在存储图的时候记录各个点的入度
  • 参考宽度优先遍历，将入度为0的点入队列
  • 将队列里的点依次出队列，然后找出以所有出队列的为始点的边，删除所有边，并将另一侧的点入度减1，若该点入度为0则入队列
  • 如果所有点都进过队列，则说明可以拓扑排序，输出顶点即可
  • 使用数组模拟队列更好，因为可以记录队列长度，以及可以记录每一个入队元素的值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool topsort(){
    int hh=0,tt=-1;
    for(int i=1;i<=n;i++)
        if(!d[i]) q[++tt]=i;
    while(hh<=tt){
        int t=q[hh++];
        for(int i=h[t];i!=-1;i=ne[i]){
            int j=e[i];
            d[j]--;
            if(!d[j]) q[++tt]=j;
        }
    }
    return tt==n-1;
}

四、最短路

最短路

最短路问题：给定一个有向图或者无向图，求一个点到另一个点的最短距离

图的存储方式选择：对于n个点，m条边的图

  • n<m && n2<=108 则为稠密图，用邻接表存储
  • n和m一个量级则为稀疏图，用邻接矩阵存储

Dijkstra算法

朴素版本O(n^2)：

核心思路：

  • 初始化距离数组，memset(d,0x3f,sizeof) d[1]=0 1⃣️
  • 经过n次循环，每次循环确定一个min加入集合st中，n次就可以得出所有点到起点的最短距离 2⃣️
  • 找到不在集合st中d[]最小的点t 3⃣️ O(n^2) -----> O(n)
  • 将t加入到集合st中去 4⃣️ O(n)
  • 用t更新t到所有其他点的距离（松弛操作） 5⃣️ O(m) ------>O(mlogn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int dijkstra(){
    // 初始化距离数组
    memset(d,0x3f,sizeof d);  
    d[1]=0;
    
    for(int i=0;i<n;i++){ //n次循环
        int t=-1;
        for(int j=1;j<=n;j++){  //找到不在集合st中d[]最小的点t 
            if(!st[j] && (t==-1 || d[t]>d[j])) t=j;
        }
        st[t]=true; //将t加入到集合st中去
        for(int j=1;j<=n;j++){  //用t更新t到所有其他点的距离
            d[j]=min(d[j],d[t]+g[t][j]); 
        }
    }
    if(d[n]==0x3f3f3f3f) return -1;// 表示到不了终点
    else return d[n];
}

堆优化版本O(mlogn)

核心思路：类比宽搜。对朴素版步骤3⃣️中寻找最小值做了优化，即使用了优先队列（堆），将其时间复杂度从O(n^2)优化到O(n)；利用堆顶来更新其他点的距离，这样步骤5⃣️中的时间复杂度变为O(mlogn)，所以总体时间复杂度为O(mlogn)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int dijkstra(){
    memset(d,0x3f,sizeof d);
    d[1]=0;
    
    priority_queue<PII,vector<PII>,greater<PII>> heap;
    heap.push({0,1});
    
    while(heap.size()){  // 类比步骤2
        // 类比步骤3找最小值
        auto t=heap.top();
        heap.pop();
        int ver=t.second,dist=t.first;  // 由于pair是按照第一个排序的，第一个要存储距离
        if(st[ver]) continue;  // 倘若该点在集合st中则不考虑
        
        st[ver]=true;   // 将该点加入st集合
        
        for(int i=h[ver];i!=-1;i=ne[i]){
            int j=e[i];
            if(d[j]>dist+w[i]){
                d[j]=dist+w[i];
                heap.push({d[j],j}); // O(longn)
            }
        }
    }
    if(d[n]==0x3f3f3f3f) return -1;
    else return d[n];
}

Bellman_Ford算法

擅长解决有负权边且有限制边数的最短路问题

核心思路：假设 1 号点到 n 号点是可达的，每一个点同时向指向的方向出发，更新相邻的点的最短距离，通过循环 n-1 次操作，若图中不存在负环，则 1 号点一定会到达 n 号点，若图中存在负环，则在 n-1 次松弛后一定还会更新

for n次

​ for 所有边

​ 松弛操作 d[b]=min(d[b],backup[a]+w)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
typedef pair<int,int> PII;
pair<PII,int> edges[M];
int n,m,k;
int d[N],backup[N]; 

int bellman_ford(){
    memset(d,0x3f,sizeof d);
    d[1]=0;
    
    for(int i=0;i<k;i++){
        memcpy(backup,d,sizeof d); // 这里使用备份数组是防止串联发生
        for(int j=0;j<m;j++){
            int a=edges[j].first.first,b=edges[j].first.second;
            int c=edges[j].second;
            d[b]=min(d[b],backup[a]+c);  //松弛操作
        }
    }
    if(d[n]>0x3f3f3f3f/2) return -1; // 在遍历所有边的时候到达d[n]可能被松弛后小于inf
    else return d[n];
}

Q1：dijkstra为啥不能处理带有负权边的最短路问题？

image-20221028131405481

A1：在上图中运用dijkstra算法求出来的最短路径是1–>2–>4–>5，然而正确的最短路径是1–>3–>4–>5

​ 故而dijkstra失效

Q2：backup数组有何用处？

image-20221028132723319

A2：在上图中，假设最多松弛一次，如果没有backup数组，结果如下：

image-20221028133011679

​ 会产生串联的后果，即在松弛了边1–>2后，d[2]=1,如果用d[2]=1来松弛节点3，那么就多了一条边，并且 d[3]=2,很显然是错误的，于是backup数组的作用在于，只用上次松弛后的结果，避免产生因使用当前松弛更新后的节点串联更新而造成限制边数+1的后果

SPFA算法（多用！！！）

使用spfa求带负权边的最短路

引入：Bellman_ford算法会遍历所有的边，但是有很多的边遍历了其实没有什么意义，我们只用遍历那些到源点距离变小的点所连接的边即可，只有当一个点的前驱结点更新了，该节点才会得到更新；因此考虑到这一点，我们将创建一个队列每一次加入距离被更新的结点。

spfa与dijkstra的区别：

  • Dijkstra算法中的st数组保存的是当前确定了到源点距离最小的点，且一旦确定了最小那么就不可逆了(不可标记为true后改变为false)；SPFA算法中的st数组仅仅只是表示的当前发生过更新的点，且spfa中的st数组可逆(可以在标记为true之后又标记为false)。顺带一提的是BFS中的st数组记录的是当前已经被遍历过的点。
  • Dijkstra算法里使用的是优先队列保存的是当前未确定最小距离的点，目的是快速的取出当前到源点距离最小的点；SPFA算法中使用的是队列(你也可以使用别的数据结构),目的只是记录一下当前发生过更新的点。

spfa与bellman–ford的区别：

  • Bellman_ford算法里最后return -1的判断条件写的是dist[n]>0x3f3f3f3f/2;而spfa算法写的是dist[n]==0x3f3f3f3f;其原因在于Bellman_ford算法会遍历所有的边，因此不管是不是和源点连通的边它都会得到更新；但是SPFA算法不一样，它相当于采用了BFS，因此遍历到的结点都是与源点连通的，因此如果你要求的n和源点不连通，它不会得到更新，还是保持的0x3f3f3f3f。
  • Bellman_ford算法可以存在负权回路，是因为其循环的次数是有限制的因此最终不会发生死循环；但是SPFA算法不可以，由于用了队列来存储，只要发生了更新就会不断的入队，因此假如有负权回路请你不要用SPFA否则会死循环。
  • 由于SPFA算法是由Bellman_ford算法优化而来，在最坏的情况下时间复杂度和它一样即时间复杂度为 O(nm)O(nm) ，假如题目时间允许可以直接用SPFA算法去解Dijkstra算法的题目。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 类比堆优化的dijkstra算法，不同在于入队和出队集合都要发生改变，也就是st的性质注意区别
int spfa(){
    memset(d,0x3f,sizeof d);
    d[1]=0;
    queue<int> q;
    q.push(1);
    st[1]=true;
    while(q.size()){
        int t=q.front();
        q.pop();
        st[t]=false;
        
        for(int i=h[t];i!=-1;i=ne[i]){
            int j=e[i];
            if(d[j]>d[t]+w[i]){
                d[j]=d[t]+w[i];
                if(!st[j]){
                    q.push(j);
                    st[j]=true;
                }
            }
        }
    }
    return d[n];
}

使用spfa判断负环：

求负环一般使用SPFA算法，方法是用一个cnt数组记录每个点到源点的边数，一个点被更新一次就+1，一旦有点的边数达到了n那就证明存在了负环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int cnt[N]; // 表示到达某个点的最短路径经过的边数
bool spfa(){
    queue<int> q;
    for(int i=1;i<=n;i++) {
        q.push(i); // 每个点都入队,因为单单从一个点开始不一定能搜到负环
        st[i]=true;
    }
    while(q.size()){
        int t=q.front();
        q.pop();
        st[t]=false;
        for(int i=h[t];i!=-1;i=ne[i]){
            int j=e[i];
            if(d[j]>d[t]+w[i]){
                d[j]=d[t]+w[i];
                cnt[j]=cnt[t]+1;  //如果更新，则cnt也要+1
                if(cnt[j]>=n) return true;
                if(!st[j]){
                    st[j]=true;
                    q.push(j);
                }
            }
        }
    }
    return false;
}

Floyd算法

本质：dp思想

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=211;
int d[N][N];
int n,m,T;

void floyd(){
    for(int k=1;k<=n;k++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
            }
        }
    }
}

int main(){
    cin>>n>>m>>T;
    memset(d,0x3f,sizeof d);
    
    // 处理重边和自环，自环为0，重边取小
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= n; j ++ )
            if (i == j) d[i][j] = 0; // 当x=y时，距离为0
    
    for(int i=0;i<m;i++){
        int a,b,c;
        cin>>a>>b>>c;
        d[a][b]=min(d[a][b],c);
    }
    
    floyd();
    
    while(T--){
        int x,y;
        cin>>x>>y;
        if(d[x][y]>0x3f3f3f3f/2) puts("impossible");
        else cout<<d[x][y]<<endl;
    }
    return 0;
}

五、最小生成树

定义：给定一张带权无向图，由n顶点和n-1条边构成的无向联通子图被称为该图的一棵生成树，其中的权值之和最小的生成树被称为无向图的最小生成树

最小生成树

prime算法

用于解决稠密图，使用邻接矩阵存储

核心思想：每次将离连通部分的最近的点和点对应的边加入的连通部分，连通部分逐渐扩大，最后将整个图连通起来，并且边长之和最小

代码可以类比朴素版dijkstra，不同点在于，dijkstra中的d数组是每个点到源点的距离，而prim中的d数组则是每个点到当前生成树的距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 注意是无向图，要存储双边，重边取小，自环不管
int pre[N]; //某个节点的前驱节点
int prim(){
    memset(d,0x3f,sizeof d);
    d[1]=0;
    int res=0;
    for(int i=0;i<n;i++){
        int t=-1;
        for(int j=1;j<=n;j++) if(!st[j] && (t==-1 || d[t]>d[j])) t=j;
        res+=d[t]; // 必须先更新
        if(d[t]==0x3f3f3f3f) return 0x3f3f3f3f;
        st[t]=true;
        for(int j=1;j<=n;j++) {
            d[j]=min(d[j],g[t][j]);  // dijkstra里面是min(d[j],d[t]+g[t][j])，注意区别
            // pre[i]=t;
        }
    }
    return res;
}

// 显示路径（倒着来）
void getPath(){
    for(int i=n;i>1;i--) {  // n个节点，n-1条边
        cout<<i<<' '<<pre[i]<<' '<<endl; // i是节点编号，pre[i]是i节点的前驱节点
    }
}

kruskal算法

核心思路：

  • 将所有边按照权值大小进行升序排序，然后从小到大遍历
  • 如果这个边的两个端点在同一集合中，说明形成了回路，舍弃；反之加入这条边，并更新集合
  • 若筛选出来的边数小于n-1，则无最小生成树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int n,m,p[N];

struct edge{ 
    int a,b,c;
    bool operator < (const edge &C) const {   // 重载 < ,按照权值排序
        return c<C.c;
    }
}edges[N];

int find(int x){
    if(x!=p[x]) p[x]=find(p[x]);
    return p[x];
}

int kruskal(){
    sort(edges,edges+m);
    for(int i=1;i<=n;i++) p[i]=i;
    int cnt=0,res=0;
    for(int i=0;i<m;i++){
        int a=edges[i].a,b=edges[i].b,c=edges[i].c;
        a=find(a),b=find(b);
        if(a!=b){
            p[a]=b;
            cnt++;
            res+=c;
        }
    }
    if(cnt<n-1) return 0x3f3f3f3f;
    else return res;
}

六、二分图

定义：

  • 有两顶点集且图中每条边的的两个顶点分别位于两个顶点集中，每个顶点集中没有边直接相连接

  • 通俗的讲，图中点通过移动能分成左右两部分，左侧的点只和右侧的点相连，右侧的点只和左侧的点相连。

重要性质：二分图一定没有奇数环

eg：

下图是二分图：

image-20240523180709601

下图不是二分图：

1.png

染色法

该算法用于判断二分图

核心步骤：

  • 开始对任意一未染色的顶点染色。

  • 判断其相邻的顶点中，若未染色则将其染上和相邻顶点不同的颜色。

  • 若已经染色且颜色和相邻顶点的颜色相同则说明不是二分图，若颜色不同则继续判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=100010,M=200010;
int e[M],ne[M],h[N],idx,color[N];
int n,m;

void add(int a,int b){
    e[idx]=b;ne[idx]=h[a],h[a]=idx++;
}

bool dfs(int u,int c){ // 深搜
    color[u]=c;  // 对该点染色
    for(int i=h[u];i!=-1;i=ne[i]){ // 遍历该点的所有相邻点
        int j=e[i];
        if(!color[j]){  // 如果没有染色，则对其染色
            if(!dfs(j,3-c)) return false; 
        }
        else if(color[j]==c) return false;  // 若该点某一相邻点已经染色且二者同色，则矛盾
    }
    return true;
}

int main(){
    cin>>n>>m;
    memset(h,-1,sizeof h);
    for(int i=0;i<m;i++){
        int a,b;
        cin>>a>>b;
        add(a,b),add(b,a); // 无向图
    }
    
    bool flag=true; 
    for(int i=1;i<=n;i++){
        if(!color[i]){ // 倘若该点没有染色
            if(!dfs(i,1)) { // 对其染色并判断有没有出现矛盾
                flag=false;
                break;
            }
        }
    }
    if(flag) puts("Yes");
    else puts("No");
    
    return 0;
}

匈牙利算法

该算法用于求二分图的最大匹配数

匹配：在图论中，一个「匹配」是一个边的集合，其中任意两条边都没有公共顶点。

最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=510,M=100010;
int e[M],ne[M],h[N],idx,；
int n1,n2,m;
int match[N]; //match[j]=a,表示女孩j的现有配对男友是a
int st[N];//st[]数组我称为临时预定数组，st[j]=a表示一轮模拟匹配中，女孩j被男孩a预定了。

void add(int a,int b){
    e[idx]=b; ne[idx]=h[a]; h[a]=idx++;
}

//这个函数的作用是用来判断,如果加入x来参与模拟配对,会不会使匹配数增多
bool find(int x)
{
    //遍历自己喜欢的女孩
    for(int i = h[x] ; i != -1 ;i = ne[i])
    {
        int j = e[i];
        if(!st[j])//如果在这一轮模拟匹配中,这个女孩尚未被预定
        {
            st[j] = true;//那x就预定这个女孩了
            //如果女孩j没有男朋友，或者她原来的男朋友能够预定其它喜欢的女孩。配对成功,更新match
            if(!match[j]||find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }
    //自己中意的全部都被预定了。配对失败。
    return false;
}

int main(){
    cin>>n1>>n2>>m;
    memset(h,-1,sizeof h);
    while(m--){
        int a,b;
        cin>>a>>b;
        add(a,b);  // 虽然是无向图，但是单向存储即可
    }
    int res=0;  //记录最大匹配
    for(int i=1;i<=n1;i++){
        memset(st,0,sizeof st);   //因为每次模拟匹配的预定情况都是不一样的所以每轮模拟都要初始化
        if(find(i)) res++;
    }
    cout<<res<<endl;
    return 0;   
}